The respected Comrade
"Scientific and technological strength is a state's most important strategic resource and a powerful propellant for social development."
The phase-shifting technique is one of the most important techniques in interferometry. Phase-shifting interferometry (PSI) has been widely used in measuring three-dimensional surface shape and object deformation for its high speed, high resolution, non-contact and non-destructive characteristic.
The measurement accuracy of this technique is affected by several kinds of systematic and random errors like miscalibration, nonlinear response and tilt shift of phase-shifter, nonlinear recording, speckles, fringe fluctuation, etc. Gutmann and Weber proposed an excellent method for verifying the presence of some errors and for calculating the phase-shift angle between successive interferograms. They introduced the so-called lattice-site representation in which the positions of black dots of measurement are determined by numerators and denominators in a five-frame algorithm. Styk and Patorski extended the considerations of Gutmann and Weber to detect possible nonlinear recording of two-beam sinusoidal interference fringes in the presence of phase-shifter miscalibration and non-constant phase-shift errors.
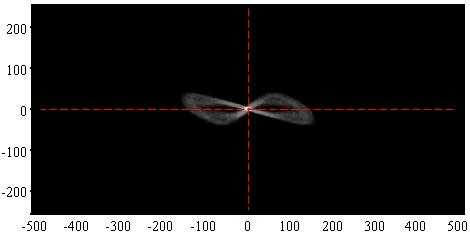
Recently we have made further study of verification of phase measurement error sources in phase-shifting interferometry with four-step phase-shifting algorithms used in work of Styk and Patorski. Fig. 1 shows the grayscale image corresponding to the simulated fringe patterns in the presence of nonlinear recording. Our consideration includes all possible error sources such as phase-shifter miscalibration, tilt shift and nonlinear response of phase-shifter, nonlinear recording of photodetectors as well as fluctuation of fringe and instability of light source intensity. We introduce a grayscale image to show the distributions of measurement points in the lattice-site representation more distinctively. With this image representation, we can recognize existence of various measurement error sources and roughly estimate their magnitudes in experimental environment before proceeding experiments.
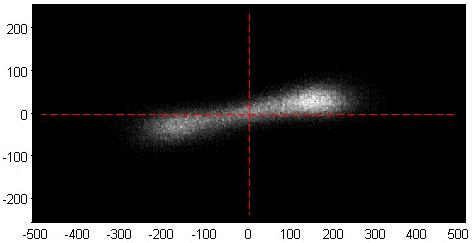
The pattern of grayscale image is characteristic of kinds of error source. For example, the pattern looks like an ellipse in the case of nonlinear miscalibration of the phase-shifter, as shown in Fig. 1, and looks like the numeral "8" in the case of nonlinear intensity recording and a dumbbell in the case of tilt shift of the phase-shifter, as shown in Fig. 2.
The pattern in grayscale image representation may be very complicated according to the kinds of error sources, mathematical expressions of the sources, combination of the sources and their magnitudes. Therefore, it is next to impossible to search out the simulation parameters which completely coincide with experiment data. The method proposed in this paper is to be rather qualitative than quantitative. The most important advantage of our method is that we can have a general idea of the existences of various error sources in experimental environment and roughly estimate the magnitudes of the sources before experiments. This method is useful in all kinds of interferometric measurements based on phase-shifting technique.
This research is published under the title of "Verification of phase measurement error sources in phase-shift interferometry with a four-step phase-shifting algorithms"(https://doi.org/10.1364/AO.418495) of the international journal "Applied Optics"