In this work, we have investigated the lattice vibration and chemical stability of the cubic inorganic halide perovskite solid solutions by appling the virtual crystal approximation (VCA) approach within density functional perturbation theory (DFPT) and the ab initio thermodynamic method.
The first principle calculations have been carried out by applying the pseudopotential plane wave program, QUANTUM ESPRESSO (QE, version 6.2) package.
Soft norm-conserving pseudopotentials of Cs, Pb, Br, I atoms were constructed using the input files provided in the pslibrary (version 1.0.0) and LD1 code included in the QE package. The pseudopotentials of virtual atoms X = I1-xBrx (x = 0.0, 0.1,..., 1.0) were constructed by averaging pseudopotentials of I, Br using the VCA. We used computational parameters: kinetic cutoff energies of 60 Ry and 480 Ry for the plane wave function and electron density, and special k points of (6 × 6 × 6) and (6 × 6 × 4) for cubic and hexagonal unit cells, respectively.
First we calculated phonon dispersions curves at 11 volumes with evenly increasing equilibrium volume, as varying the Br content x in the solid solutions CsPbX3, CsX, and PbX2. Then we calculated the entropy and Helmholtz free energy (F) within the quasiharmonic approximation from the obtained phonon dispersions curves. The enthalpy was calculated by fitting Helmholtz free energy curves versus volume data to the solid state equation. Then Gibbs free energy of the solid solutions, G = U – TS + PV, was calculated at each Br content x. The chemical stability of halide solid solution CsPbX3 was evaluated by calculating Gibbs free energy differences for decomposition reaction CsPbX3 = CsX + PbX2. It means that if Gibbs free energy differences are negative, the compounds are stable against the chemical decomposition and if Gibbs free energy differences are positive, they are decomposed.
Then we calculated phonon dispersions curves of cubic solid solutions CsPbX3, CsX and hexagonal solid solution PbX2. Through calculations of phonon dispersions, we observed the soft phonon modes for solid solution CsPbX3 containing halide PbX6 octahedra. These soft phonon modes were formed due to structural instabilities associated with the distortion or tilting of PbX6 octahedra. The soft phonon modes weren't observed because cubic CsX hasn't halide octahedral. For the case of perovskite solid solutions CsPbX3, we observed soft phonon modes at the Brillouin zone (BZ) boundary (R, M, X), which are relative to antiferroelectricity due to a cancellation of opposing polarizations induced in neighbor unit cells.
The distortion of halide octahedral was also appeared at the zone center, which originates ferroelectricity. It was accepted that these vibrational instabilities could be caused by the interaction between Cs and X atoms and stabilized by anharmonic processes at high temperature, providing phase transition. It is found that as increasing Br content x, the phonon energies gradually increase.
Then we calculated Gibbs free energy differences of the solid solutions to evaluate stabilities upon the chemical decomposition of the solid solutions under the limited temperature and pressure.
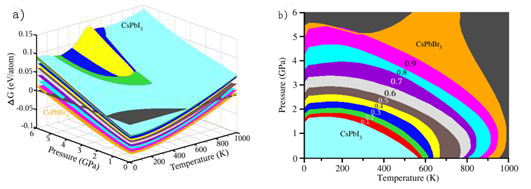
From the three-dimensional plot(Fig. (a)) of Gibbs free energy differences ΔG(T,P) in the temperature range of 0–1 000 K and the pressure range of 0–6 GPa, it is revealed that the theoretical maximum temperature with stabilities for the solid solutions CsPbX3 increases as Br content x increases under the same pressure. For the case of cubic CsPbI3, when pressure is fixed at 0 Pa, free energy differences indicate negative values at temperature range of 0–560 K, in which the solid solutions are stable upon the chemical decomposition, in good agreement with previous work. As shown in Fig. (b), the stable temperature range upon chemical decomposition was enhanced as increasing the Br content x and the temperature range was calculated to be 0–1 000 K.
Our results was published in the journal of PHYSICAL REVIEW MATERIALS(Vol.4, 045402, 2020, pp.1-9) with the title of "First-principles study on material properties and stability of inorganic halide perovskite solid solutions CsPb(I1-xBrx)3" (https://doi.org/10.1103/PhysRevMaterials.4.045402).