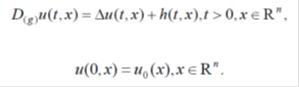The respected Comrade
"Scientific and technological strength is a state's most important strategic resource and a powerful propellant for social development."
The fractional differential equation has recently become an effective tool of modeling complex nonlinear phenomena in fluid mechanics, life science, quantum mechanics, ecosystem theory, and so on.
We studied the initial value problem of the generalized fractional diffusion equation as follows.
Here D(g) is a generalized Caputo fractional differential operator.
The equation effectively describes the anomalous diffusion phenomena that exist in various forms in the real world. Today the anomalous diffusion process has attracted great attention of the academic community as it is observed in important physical processes including life activity. In particular, the equation is derived from continuous time random walk theory, a powerful theoretical tool to explain complex systems.
In the previous work, supposing the Holder continuity as an initial condition, the representation formula of solutions for the initial value problem was obtained when h=0. The solution is twice continuously differentiable with respect to the space variable x. From the physical point of view, it is not necessary that the solution u(t,x) is twice continuously differentiable with respect to the space variable x. In fact, when the diffusion equation is derived, it is assumed that the solution u(t,x) is not only Laplace transformable with respect to t, but also Fourier transformable with respect to x. Also, the previous paper indicated that the results regarding the asymptotic behavior of the solution of the equation have not yet been solved.
We investigated the existence of Fourier transformable solutions and the asymptotic behavior under weak assumptions for the initial conditions in this case of h≠0. As is well known, the Fourier analysis is a very effective tool in studying partial differential equations. We have proved the representation formula of solutions of the initial value problem by using important principles of the Fourier analysis theory including Young's inequality. We also find important properties of the solution such as boundedness, positivity and various norm estimates. In particular, the results for the asymptotic behavior are in good agreement with the results which were already proved in the literature for special cases of the kernel function g.
The paper entitled "The Cauchy problem for general time fractional diffusion equation" (https://doi.org/10.1515/fca-2020-0077), which introduce our new results, has been published in the SCI journal "Fractional Calculus & Applied Analysis" 23(2020).
In this paper, we proved the unique existence and the asymptotic behavior of the solution of the initial value problem for the generalized time-fractional diffusion equation in modeling the anomalous diffusion phenomenon by employing the Fourier analytical theory. In contrast to the previous work, in this paper, we considered the existence and long-time behavior of the solution under the weaker assumptions about the initial conditions when the nonhomogeneous term was added.