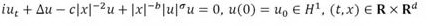The respected Comrade
"Scientific and technological strength is a state's most important strategic resource and a powerful propellant for social development."
We studied the Cauchy problem for the inhomogeneous nonlinear Schrödinger (INLSc) equation with inverse square potential:
Where d≥3 and 0
The INLSc equation appears in a variety of physical settings, for example, in nonlinear optical systems with spatially dependent interactions. The case b=c=0 is the classic nonlinear Schrödinger (NLS) equation which has been widely studied over the last three decades. The case b=0 and c≠0 is known as the NLS equation with inverse-square potential, denoted by NLSc equation, which has also been extensively studied in recent years. Moreover, when c=0 and b≠0, we have the inhomogeneous nonlinear Schrödinger equation, denoted by INLS equation, which has also attracted a lot of interest in recent years.
Recently, Campos-Guzmán [Z. Angew. Math. Phys. 72 (2021) 143] studied the global existence and blow-up of solutions to the focusing INLSc equation in the intercritical case. However, they only treat the data below the ground state threshold. In particular, the blow-up result was shown only for radial or finite variance data. Later, Dinh-Keraani [SIAM J. Math. Anal. 53 (2021) 4765–4811] systematically studied the long time dynamics of solutions to the focusing intercritical INLS equation with general (not necessarily radial or finite variance) data lying below, at, and above the ground state threshold.
Motivated by these papers, we studied the global existence and blow-up of solutions to the focusing intercritical INLSc equation with general (not necessarily radial or finite variance) data lying below, at, and above the ground state threshold. We first established the criteria for global existence and blow-up of general solutions to the equation. Using these criteria, we then studied the global existence and blow-up of solutions to the equation with general data lying below, at, and above the ground state threshold. Our results can be seen as the extension of the global existence and blow-up results of [SIAM J. Math. Anal. 53 (2021) 4765–4811] to the focusing intercritical INLSc equation. Our results also extend the ones of [Z. Angew. Math. Phys. 72 (2021) 143] by treating the general data lying not only below the ground state threshold but also at, and above the ground state threshold.
The detailed result was published in "Discrete and Continuous Dynamical Systems-Series B 28(2) (2023) 1046-1067" under the title of "Global existence and blow-up for the focusing inhomogeneous nonlinear Schrödinger equation with inverse-square potential" (https://doi.org/10.3934/dcdsb.2022111).