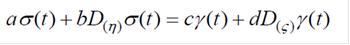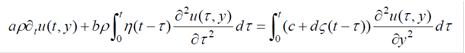《대학에서는 사회주의강국건설에서 나서는 리론실천적, 과학기술적문제들을 원만히 해결하며 기초과학부문을 발전시키고 첨단과학기술분야를 개척하는데 중심을 두고 과학연구사업을 진행하여야 합니다.》
오늘날 분수계미분연산자는 류체력학에서 중요한 자리를 차지하는 류체의 점탄성구성관계를 수학적으로 모형화하는데서 효과적인 수단으로 되고있다. 현실에 존재하는 적지 않은 류체들의 점탄성구성관계가 분수계미분연산자에 의하여 효과적으로 모형화되였다. 하지만 점탄성류체의 다양성과 점탄성구성관계의 복잡성은 새로운 형식의 수학적모형들을 계속 요구한다.
우리는 우선 다음과 같은 일반적인 형식의 점탄성구성방정식을 제기하였다.
여기서 D(g)는 일반화된 캐푸토분수계미분연산자이다. 이 구성관계는 이미 존재하는 여러가지 형식의 점탄성구성방정식들을 포함한다.
다음으로 두개의 무한평행평판사이에서 흐르는 일반화된 구성관계를 가진 점탄성류체의 운동을 고찰하였다. 일명 꾸에트흐름으로 불리우는 이 류체흐름은 공학실천에서 자주 나타나는것으로 하여 중요하게 연구되고있다. 일반화된 점탄성구성관계를 가진 점탄성류체의 꾸에트흐름에 대한 운동방정식은 다음과 같은 형식의 적분미분방정식으로 표시된다.
또한 연산자방법을 리용하여 일반화된 점탄성구성관계의 특수한 경우들에 대응하는 적분미분방정식의 해석적풀이들을 다변수미타그-레플레르함수에 의하여 표시하였다.
우리는 연구결과를 Wiley출판사의 잡지 《Mathematical methods in the applies sciences》 43(2020)에 《Couette flow of viscoelastic fluid with constitutive relation involving general Caputo-type fractional derivatie》 (https://doi.org/10.1002/mma.5911)의 제목으로 발표하였다.
이 론문에서는 일반화된 캐푸토분수계미분연산자를 리용하여 일반화된 점탄성구성관계를 제기하고 이 구성관계를 가진 점탄성류체의 두 평행평판사이에서의 흐름방정식을 유도하였으며 특수한 경우들에 대응하는 운동방정식의 해석적풀이들을 구하고 류체의 속도마당을 그라프로 보여주었다.