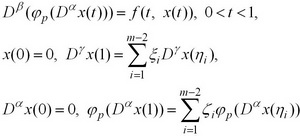최근년간 분수계미분방정식이 물리학, 화학, 생물학, 재료과학, 천문학, 인공지능 등 자연과 사회, 인간생활의 넓은 범위에서 일어나는 많은 현상들을 모의하는 한가지 중요한 수단으로 발전함에 따라 이에 대한 수학적인 연구도 깊이있게 진행되고있다.
우리는 다공성매질에서 류체의 막흐름을 모형화하는 p-라쁠라스분수계미분방정식의 여러점경계값문제
에 대한 수치해석적연구를 진행하였다. 여기서 α, β, γ는 1<α, β≤2, 0<γ<1을 만족시키는 상수들이며 Dα, Dβ, Dγ들은 모두 리만-류빌분수계도함수들이다. 그리고 ξi, ηi, ζi들은 0<ξi, ηi, ζi<1, i=1, 2, ∙∙∙, m-2을 만족시키며 함수 f는 [0, 1]×[0, +∞)에서 련속인 비부값함수, φp(s)=|s|p-2, p>1이다.
우리는 p-라쁠라스분수계미분방정식의 여러점경계값문제를 풀기 위한 근사풀이법을 연구하였다. 연구에서는 점배치법과 부동점반복법, 분수계적분의 하르웨블레트연산행렬을 결합시켜 p-라쁠라스연산자를 가진 분수계미분방정식의 여러점경계값문제에 대한 정인 풀이를 계산하기 위한 수값계산도식을 확립하고 도식에 의한 풀이의 정확한 풀이에로의 수렴성을 증명하였다. 부동점반복법과 PC[0, 1], C[0, 1]에서의 하르웨블레트함수근사, 분수계적분함수근사를 교대적으로 결합하여 리용함으로써 [AMC, 220 (2013) 659-667]에서 제기한 분수계비선형진동자방정식의 수값풀이법을 p-라쁠라스분수계미분방정식의 경우에로 확장하였다.
연구결과는 잡지 《Applied Numerical Mathematics》(Volume 160, 2021, 313-330)에 《A new approach for solving one-dimensional fractional boundary value problems via Haar wavelet collocation method》(https://doi.org/10.1016/j.apnum.2020.10.019)의 제목으로 출판되였다.