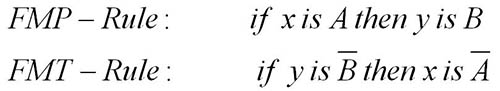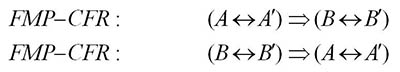《자연과학부문에서는 식량문제, 에네르기문제를 비롯하여 인민경제발전과 국방력강화에서 절박하게 나서는 과학기술적문제들을 푸는데 적극 이바지하며 기초과학과 첨단과학기술부문에서 세계적인 경쟁력을 가진 연구성과들을 내놓아야 합니다.》
1965년에 자데가 모호모임론을 내놓고 모호긍정법과 모호부정법을 제안하였으며 추론의 합성규칙(Compositional Rule of Inference: CRI)에 기초한 모호추론방법을 발견함으로써 인간의 사유과정을 공학적으로 보다 더 정확하게 모형화할수 있게 되였다.
일반적으로 모호규칙은 식 (1)의 형식으로 표현된다.
환원성은 if-then형식의 지식 혹은 규칙이 인간의 머리속에 축적되여있고 여기에 새로운 사실정보 혹은 새로운 전제가 주어졌을 때 추론결과가 전제에 상응하게 얻어지는 추론의 성질을 말한다. 환원성은 모호추론결과가 만족해야 할 가장 중요한 성질의 하나이다.
우리는 선행한 모호추론방법들에 비하여 환원성을 보다 더 잘 만족하는 새로운 모호추론방법인 보상형모호추론방법을 제안하였다.
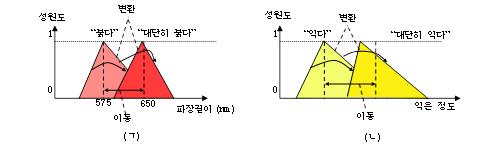
보상형모호추론(CFR)의 기본적인 착상은 전건부모호모임과 관측값사이의 이동, 변환, 이동 및 변환관계에 대응하게 결론부의 모호모임을 이동하고 변환시켜 추론결과를 얻는것이다. 이것은 인간의 사고에 부합될뿐만아니라 모호추론의 환원성도 만족한다.
(ㄱ) 전건부의 이동 및 변환 (ㄴ) 후건부의 이동 및 변환
식 (2)는 새로운 추론결과 가 전건부모호모임 와 관측 사이의 이동과 변환연산에 의하여 대응하여 후건부모호모임 를 이동시키고 변환되게 함으로써 얻어진다는것을 의미한다.
CFR에 기초한 모호긍정법은 표 1에서 보여준 모호추론의 정성적인 규준들을 만족시킨다.
또한 CFR에 기초한 모호부정법은 표. 2에서 보여준 모호추론의 정성적인 규준들을 만족시킨다.
CFR를 리용할 때 강수량예측을 위한 모호신경망의 학습시간은 스게노의 방법보다 약 5.2배 더 빠르며 학습정확도는 7.35% 개선되였다.
연구결과는 국제학술잡지인 《Iranian Journal of Fuzzy Systems》(2019, 16(3), 17-34)에 《A fuzzy reasoning method based on compensating operation and its application to fuzzy systems》 (https://ijfs.usb.ac.ir/10.22111/IJFS.2018.4175)의 제목으로 출판되였다.