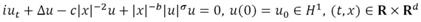《과학기술력은 국가의 가장 중요한 전략적자원이며 사회발전의 강력한 추동력입니다.》
우리는 거꿀두제곱포텐샬을 가진 비등질비선형슈뢰딩게르(INLSc)방정식의 꼬쉬문제
을 연구하였다. 여기서 d≥3이고 0
INLSc방정식은 공간적으로 호상작용하는 비선형광학계를 비롯한 물리학의 여러 분야에서 출현한다. b=c=0인 경우는 지난 30여년간 연구되여오는 고전적인 비선형슈뢰딩게르(NLS)방정식이다. b=0이고 c≠0인 경우는 NLSc방정식으로 표시되는 거꿀두제곱포텐샬을 가진 NLS방정식으로 알려져있으며 이 역시 최근년간 광범히 연구되고있다. 더우기 c=0이고 b≠0인 경우 INLS방정식으로 표시되는 비등질비선형슈뢰딩게르방정식을 얻는바 이 역시 최근년간 많은 흥미를 끌고있다.
최근 [Z. Angew. Math. Phys. 72 (2021) 143]에서는 질량초림계-에네르기준림계인 경우 집초INLSc방정식의 풀이의 대역적존재성과 폭발성을 연구하였다. 그러나 그들은 바닥상태림계값웃준위의 자료만을 론의하였다. 특히 구면대칭이거나 유한변동인 자료에 대해서만 폭발성을 연구하였다. 그후 [SIAM J. Math. Anal. 53 (2021) 4765–4811]에서는 바닥상태림계값웃준위와 같은 준위, 아래 준위에 놓이는 (반드시 구면대칭이거나 유한변동이 아닌) 일반적인 자료에 대하여 집초질량초림계-에네르기준림계INLS방정식의 풀이의 긴시간동태를 체계적으로 연구하였다.
우리는 바닥상태림계값웃준위와 같은 준위, 아래 준위에 놓이는 (반드시 구면대칭이거나 유한변동이 아닌) 일반적인 자료에 대하여 집초질량초림계-에네르기준림계INLSc방정식의 풀이의 대역적존재성과 폭발성을 연구하였다.
우선 방정식의 일반적인 풀이의 대역적존재성과 폭발성에 관한 판별식을 얻었다.
다음으로 이 판별식을 리용하여 바닥상태림계값웃준위와 같은 준위, 아래 준위에 놓이는 일반적인 자료에 대하여 방정식의 풀이의 대역적존재성과 폭발성을 연구하였다.
우리의 결과는 [SIAM J. Math. Anal. 53 (2021) 4765–4811]의 대역적존재성과 폭발성결과의 집초질량초림계-에네르기준림계INLSc방정식에로의 확장으로 볼수 있다. 우리의 결과는 또한 바닥상태림계값 아래준위뿐 아니라 같은 준위와 웃준위의 일반적인 자료를 고찰함으로써 [Z. Angew. Math. Phys. 72 (2021) 143]의 결과를 확장한다.
구체적인 결과는 잡지 《Discrete and Continuous Dynamical Systems-Series B》(28(2) (2023) 1046-1067)에 《Global existence and blow-up for the focusing inhomogeneous nonlinear Schrödinger equation with inverse-square potential》(https://doi.org/10.3934/dcdsb.2022111)의 제목으로 출판되였다.